Inside M4 chips: Matrix processing and Power Modes
For much of the last four years, CPU and GPU core performance have been of primary importance to those using Apple silicon Macs. Despite that, special interest has developed in those cores that Apple doesn’t talk about, in its matrix co-processor, AMX. Since the first M1 it has been believed that each CPU core cluster has its own AMX, and more recently it has been shown to be capable of impressive performance. With the increasing prominence of computationally intensive features including AI, this is growing in importance.
When the M4 first became available in iPads earlier this year, researchers concluded its chip has a new AMX co-processor that can now be programmed using SME matrix extensions supported by the new version of the Arm instruction set in the M4, ARMv9.2-A. The best accounts of that challenging work are given on the Friedrich Schiller University’s site Hello SME, and Taras Zakharko’s GitHub.
From early work by Dougall Johnson on the M1, it has been known that some of the functions in Apple’s vast Accelerate maths libraries can run code on the AMX. Thanks to the guidance of Maynard Handley, a year ago I concluded that one of those is the vDSP_mmul function in the vDSP sub-library. This article reports tests of that function in a Mac mini M4 Pro running Sequoia 15.1.1, leads on to an explanation of previous results using floating point and NEON tests, and considers the effects of Power Modes.
Methods
I used the same methods as described previously. These consist of running many tight loops of test code designed to be confined as much as possible to register access. The test used here uses vDSP_mmul, multiplying two 16 x 16 32-bit floating point matrices, and consists of 15 x 10^6 such loops. Its source code is given in the Appendix at the end. During each test run, the command tool powermetrics gathers core power and performance data in sampling periods of 0.1 second for a total of 50 samples. Its output is piped into a text file, which is then analysed using Numbers and DataGraph.
For comparison, I also show here my results from equivalent tests using assembly code for the NEON vector processor, as given in that previous article.
Power used by thread
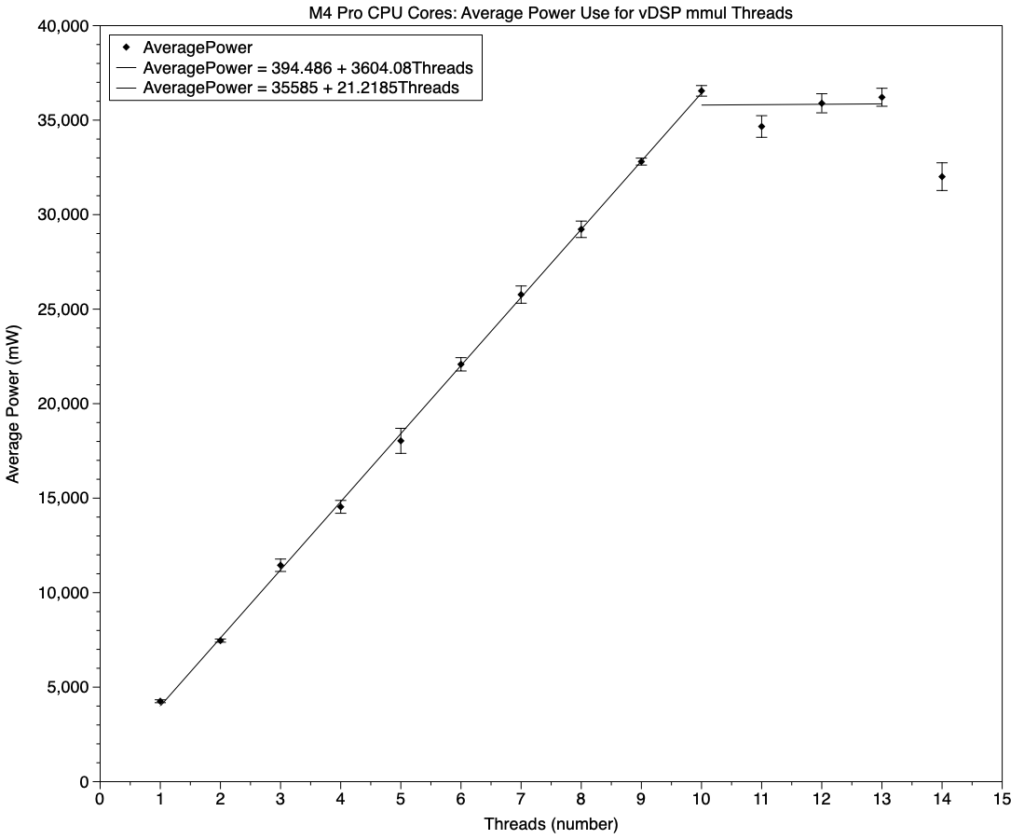
The first graphs show average power use during each test with increasing numbers of threads, where error bars indicate a spread of +1 standard deviation.
The linear relationship for 1-10 threads, run on 1-10 P cores, is a better fit for vDSP_mmul, shown above, than NEON below. Run on P cores, each vDSP_mmul thread used about 3.6 W, significantly greater than NEON at 3.0 W. However, when those high QoS threads spilt over onto E cores, that relationship for vDSP_mmul broke down, leaving the highest power use that for 10 threads, one for each P core available in the M4 Pro chip used.
There’s no evidence of the steps seen below in NEON at 2-3 and 7-8 threads.
Execution time
Total execution time has a strongly linear relationship too, for vDSP_mmul at about 2.6 seconds per thread. Again, that relationship broke down once test threads had spilt over onto E cores, unlike in the graph below for NEON.
There are also obvious differences in the time required to execute each thread. vDSP_mmul (above) showed a linear increase from 1-5 threads, followed by a constant time for 5-10 threads. Once threads were running on E cores, the relationship became far looser, as seen in the red regression line. In NEON below, the relationship was weakest in the 1-5 thread range, and closer on the E cores from 11-14 threads.
Energy use
When run on P cores, there’s a good line of fit indicating energy use of 9.2 J per thread (above), compared with NEON (below) at 7.7 J. The red line of best fit for the E core section from 11-14 cores suggests E core energy use of about 4.8 J per thread, again higher than NEON, which shows a much better fit and only about 3 J per thread.
Maximum total energy use estimated for vDSP_mmul was just over 140 J, while for NEON it was only about 90 J.
The overall picture of vDSP_mmul is thus different from those seen in floating point and NEON tests. When run on P cores alone, vDSP_mmul behaves more linearly, using significantly more power and energy. Once running threads on E cores, though, that breaks down and performance falls, rather than simply slowing.
The role of frequency
There has long been a tacit assumption that, when running on P cores, computationally intensive threads such as those used in these tests are run at a fairly constant frequency close to maximum. Looking back at my earlier results on M1 and M3 cores, though, frequencies aren’t so consistent, and in many cases not that close to maximum either.
powermetrics provides more frequency figures than you know what to do with, although most are derived and to some extent imaginary, making reconciliation difficult. Taking the best estimate of core frequency as that given as Cluster HW active frequency, patterns seen on M4 P cores are distinctive.
This graph shows those frequencies for the active P cluster by the number of threads, for floating point, NEON and vDSP_mmul tests. Frequencies for the first two are identical, at P core maximum for a single thread, then falling sharply from 2 to 3 threads. When more threads are run, the cluster that’s fully active is run at the same frequency as that for 5 threads (P cluster size on this M4 Pro), while the other P cluster follows the same frequencies shown in the graph for the number of threads it’s running.
Frequencies are controlled by macOS, and this suggests it adopts a standard pattern when running the two in-core tests, and a different one for vDSP_mmul presumably geared to performance of the AMX. Changes in frequency also account for the steps seen at 2-3 and 7-8 (= 5+2 and 5+3) threads in the NEON graphs above.
Power Modes
There has been considerable interest in the Power Mode setting available in macOS when running on M4 Pro and Max chips. To assess its effects I ran tests in 10 threads to fully occupy the P cores, at each of the three Power mdes.
There was no difference between results for the default Automatic and High Power modes, as expected. This is because the effect of High Power mode isn’t to change frequencies or power use in the short-term, but by more aggressive fan use enabling higher frequencies to be sustained for prolonged periods, when in Automatic mode they would be throttled.
Low Power does have substantial effects on core frequency, performance and power use, though. When running floating point tests in 10 threads, their cluster frequency was reduced from 3,852 to 3,624, 94% of Automatic and High Power. That reduced power use from a mean of 13.9 W to 11.2 W, and increased the time to complete threads. Time taken by floating point threads increased to 106% of Automatic and High, while that for NEON increased to 135% and vDSP_mmul to 177%. While the reduced performance for floating point threads is unlikely to be noticeable, for vector and matrix threads that’s likely to obvious to the user.
Key information
vDSP_mmul matrix multiplication from the vDSP sub-library in Accelerate behaves consistently with it being performed in the AMX co-processors in M4 Pro chips.
vDSP_mmul threads used significantly more power than NEON, reaching a maximum of just over 36 W when fully occupying all 10 P cores.
When spilt over to E cores, vDSP_mmul threads were much slower and their performance erratic, consistent with the E cluster having a smaller and significantly less performant AMX.
In-core tests (floating point and NEON) show common frequency regulation according to the number of cores active in each P core cluster. This runs a single thread at maximum frequency, then reduces sharply from 2 to 3 threads/cores. This accounts for the deviations from linearity observed in power use and performance. That pattern doesn’t appear in vDSP_mmul threads, though.
High Power and Automatic modes are identical in short-term tests.
Low Power mode reduces P cluster frequency and power use. Although its effects are unlikely to be noticeable in floating point threads, effects on vector and matrix threads are greater, and performance reductions are likely to be obvious to the user.
Previous articles
Inside M4 chips: P cores
Inside M4 chips: P cores hosting a VM
Inside M4 chips: E and P cores
Inside M4 chips: CPU core performance
Inside M4 chips: CPU power, energy and mystery
Finding and evaluating AMX co-processors in Apple silicon chips (M1 and M3)
Appendix: Source code
16 x 16 32-bit floating point matrix multiplication
var theCount: Float = 0.0
let A = [Float](repeating: 1.234, count: 256)
let IA: vDSP_Stride = 1
let B = [Float](repeating: 1.234, count: 256)
let IB: vDSP_Stride = 1
var C = [Float](repeating: 0.0, count: 256)
let IC: vDSP_Stride = 1
let M: vDSP_Length = 16
let N: vDSP_Length = 16
let P: vDSP_Length = 16
A.withUnsafeBufferPointer { Aptr in
B.withUnsafeBufferPointer { Bptr in
C.withUnsafeMutableBufferPointer { Cptr in
for _ in 1…theReps {
vDSP_mmul(Aptr.baseAddress!, IA, Bptr.baseAddress!, IB, Cptr.baseAddress!, IC, M, N, P)
theCount += 1
} } } }
return theCount
Apple describes vDSP_mmul() as performing “an out-of-place multiplication of two matrices; single precision.” “This function multiplies an M-by-P matrix A by a P-by-N matrix B and stores the results in an M-by-N matrix C.”