Inside M4 chips: CPU core performance
There’s no doubt that the CPUs in M4 chips outperform their predecessors. General-purpose benchmarks such as Geekbench demonstrate impressive rises in both single- and multi-core results, in my experience from 3,191 (M3 Pro) to 3,892 (M4 Pro), and 15,607 (M3 Pro) to 22,706 (M4 Pro). But the latter owes much to the increase in Performance (P) core count from 6 to 10. In this series I concentrate on much narrower concepts of performance in CPU cores, to provide deeper insight into topics such as core types and energy efficiency. This article examines the in-core performance of P and E cores, and how they differ.
P core frequencies have increased substantially since the M1. If we set that as 100%, M3 P cores run at around 112-126% of that frequency, and those in the M4 at 140%.
E cores are more complex, as they have at least two commonly used frequencies, that when running low Quality of Service (QoS) threads, and that when running high QoS threads that have spilt over from P cores. Low QoS threads are run at 77% of M1 frequency when on an M3, and 105% on an M4. High QoS threads are normally run at higher frequencies of 133% on the M3 E cores (relative to the M1 at 100%), but only 126% on the M4.
Methods
To measure in-core performance I use a GUI app wrapped around a series of loading tests designed to enable the CPU core to execute that code as fast as possible, and with as few extraneous influences as possible. Of the seven tests reported here, three are written in assembly code, and the others call optimised functions in Apple’s Accelerate library from a minimal Swift wrapper. These tests aren’t intended to be purposeful in any way, nor to represent anything that real-world code might run, but simply provide the core with the opportunity to demonstrate how fast it can be run at a given frequency.
The seven tests used here are:
64-bit integer arithmetic, including a MADD instruction to multiply and add, a SUBS to subtract, an SDIV to divide, and an ADD;
64-bit floating point arithmetic, including an FMADD instruction to multiply and add, and FSUB, FDIV and FADD for subtraction, division and addition;
32-bit 4-lane dot-product vector arithmetic (NEON), including FMUL, two FADDP and a FADD instruction;
simd_float4 calculation of the dot-product using simd_dot in the Accelerate library.
vDSP_mmul, a function from the vDSP sub-library in Accelerate, multiplies two 16 x 16 32-bit floating point matrices, which in M1 and M3 chips appears to use the AMX co-processor;
SparseMultiply, a function from Accelerate’s Sparse Solvers, multiplies a sparse and a dense matrix, that may use the AMX co-processor in M1 and M3 chips.
BNNSMatMul matrix multiplication of 32-bit floating-point numbers, here in the Accelerate library, and since deprecated.
Source code of the loops is given in the Appendix.
The GUI app sets the number of loops to be performed, and the number of threads to be run. Each set of loops is then put into the same Grand Central Dispatch queue for execution, at a set Quality of Service (QoS). Timing of thread execution is performed using Mach Absolute Time, and the time for each thread to be executed is displayed at the end of the tests.
I normally run tests at either the minimum QoS of 9, or the maximum of 33. The former are constrained by macOS to be run only on E cores, while the latter are run preferentially on P cores, but may spill over to E cores when no P core is available. All tests are run with a minimum of other activities on that Mac, although it’s not unusual to see small amounts of background activity on the E cores during test runs.
The number of loops completed per second is calculated for two thread totals for each of the three execution contexts. Those are:
P cores alone, based on threads run at high QoS on 1 and 10 P cores;
E cores at high frequency (‘fast’), run at high QoS on 10 cores (no threads on E cores) and 14 (4 threads on E cores);
E cores at low frequency (‘slow’), run at low QoS on 1 and 4 E cores.
Results are then corrected by removing overhead estimated as the rate of running empty loops. Finally, each test is expressed as a percentage of the performance achieved by the P cores in an M1 chip. Thus, a loop rate double that achieved by running the same test on an M1 P core is given as 200%.
P core performance
As in subsequent sections, these are shown in the bar chart below, in which the pale blue bars are for M1 P cores, dark blue bars for M3 P cores, and red for M4 P cores.
As I indicated in my preview of in-core performance, there is little difference between integer performance between M3 and M4 P cores, but a significant increase in floating point, which matches that expected by the increased frequency in the M4.
Vector performance in the NEON and simd dot tests, and matrix multiplication in vDSP mmul rise higher than would be expected by frequency differences alone, to over 160% of M1 performance. The latter two tests are executed using Accelerate library calls, so there’s no guarantee that they are executed the same on different chips, but the first of those is assembly code using NEON instructions. SparseMultiply and BNNS matmul are also Accelerate functions whose execution may differ, and don’t fare quite as well on the M4.
E core slow performance
On E cores, threads run at low QoS are universally at frequencies close to idle, as reflected in their performance, still relative to an M1 P core at much higher frequency. Frequency differences account for the relatively poor performance of M3 E cores, and improvement in results for the M4. Those are disproportionate in vector and matrix tests, which could be accounted for by the M4 E core running those at higher frequencies than would be normal for low QoS threads.
Although the best of these, NEON, is still well below M1 P core performance (73%), this suggests a design decision to deliver faster vector processing on M4 E cores, which is interesting.
E core fast performance
Ideally, when high QoS threads overspill from P cores, it’s preferable that they’re executed as fast as they would have been on a P core. Those in the M1 fall far short of that, in scalar and vector tests only delivering 40-60% of a P core, although that seemed impressive at the time. The M3 does considerably better, with vector and one matrix test slightly exceeding the M1 P core, and the M4 is even faster in vector calculations, peaking at over 130% for NEON assembly code.
Far from being a cut-down version of its P core, the M4 E core can now deliver impressive vector performance when run up to maximum frequency.
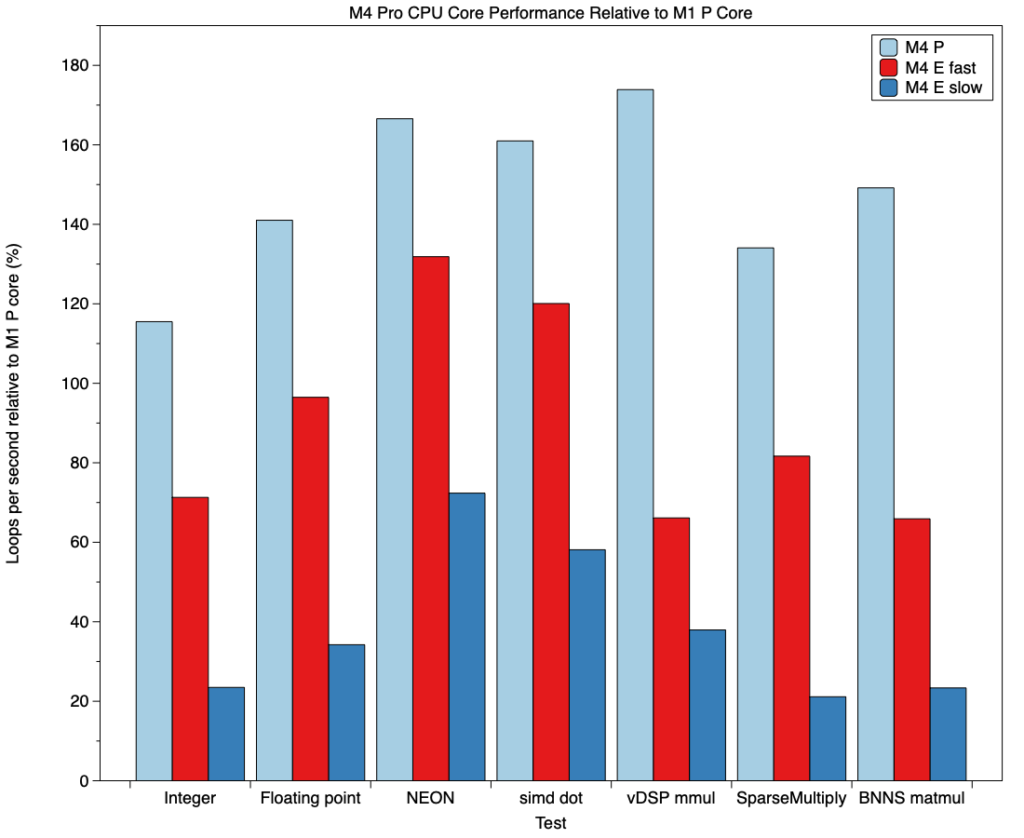
M4 P and E comparison
Having considered how P and E cores have improved against those in the M1, it’s important to look at the range of computing capacity they provide in the M4. This is shown in the chart below, where pale blue bars are P cores, red bars E cores at high QoS and frequency, and dark blue bars E cores at low QoS and frequency. Again, these are all shown relative to P core performance in the M1.
Apart from the integer test, scalar floating point, vector and matrix calculations on P cores range between 140-175% those of the M1, a significant increase on those expected from frequency increase alone. Scalar and vector (but not matrix) calculations on E cores at high frequency are slower, although in most situations that shouldn’t be too noticeable. Performance does drop off for E cores at low frequency, though, and would clearly have impact for code.
Given the range of operating frequencies, P and E cores in the M4 chip deliver a wide range of performance at different power levels, and its power that I’ll examine in the next article in this series.
Key information
M4 P core maximum frequency is 140% that of the M1. That increase in frequency accounts for much of the improved P core performance seen in M4 chips.
E core frequency changes are more complex, and some have reduced rather than risen compared with the M1.
P core floating point performance in the M4 has increased as would be expected by frequency change, and vector and matrix performance has increased more, to over 160% those of the M1.
E core performance at low QoS and frequency has improved in comparison to the M3, and most markedly in vector and matrix tests, suggesting design improvements in the latter.
E core performance at high QoS and frequency has also improved, again most prominently in vector tests.
Across their frequency ranges, M4 P and E cores now deliver a wide range of performance and power use.
Previous articles
Inside M4 chips: P cores
Inside M4 chips: P cores hosting a VM
Inside M4 chips: E and P cores
Appendix: Source code
_intmadd:
STR LR, [SP, #-16]!
MOV X4, X0
ADD X4, X4, #1
int_while_loop:
SUBS X4, X4, #1
B.EQ int_while_done
MADD X0, X1, X2, X3
SUBS X0, X0, X3
SDIV X1, X0, X2
ADD X1, X1, #1
B int_while_loop
int_while_done:
MOV X0, X1
LDR LR, [SP], #16
RET
_fpfmadd:
STR LR, [SP, #-16]!
MOV X4, X0
ADD X4, X4, #1
FMOV D4, D0
FMOV D5, D1
FMOV D6, D2
LDR D7, INC_DOUBLE
fp_while_loop:
SUBS X4, X4, #1
B.EQ fp_while_done
FMADD D0, D4, D5, D6
FSUB D0, D0, D6
FDIV D4, D0, D5
FADD D4, D4, D7
B fp_while_loop
fp_while_done:
FMOV D0, D4
LDR LR, [SP], #16
RET
_neondotprod:
STR LR, [SP, #-16]!
LDP Q2, Q3, [X0]
FADD V4.4S, V2.4S, V2.4S
MOV X4, X1
ADD X4, X4, #1
dp_while_loop:
SUBS X4, X4, #1
B.EQ dp_while_done
FMUL V1.4S, V2.4S, V3.4S
FADDP V0.4S, V1.4S, V1.4S
FADDP V0.4S, V0.4S, V0.4S
FADD V2.4S, V2.4S, V4.4S
B dp_while_loop
dp_while_done:
FMOV S0, S2
LDR LR, [SP], #16
RET
func runAccTest(theA: Float, theB: Float, theReps: Int) -> Float {
var tempA: Float = theA
var vA = simd_float4(theA, theA, theA, theA)
let vB = simd_float4(theB, theB, theB, theB)
let vC = vA + vA
for _ in 1…theReps {
tempA += simd_dot(vA, vB)
vA = vA + vC
}
return tempA
}
16 x 16 32-bit floating point matrix multiplication
var theCount: Float = 0.0
let A = [Float](repeating: 1.234, count: 256)
let IA: vDSP_Stride = 1
let B = [Float](repeating: 1.234, count: 256)
let IB: vDSP_Stride = 1
var C = [Float](repeating: 0.0, count: 256)
let IC: vDSP_Stride = 1
let M: vDSP_Length = 16
let N: vDSP_Length = 16
let P: vDSP_Length = 16
A.withUnsafeBufferPointer { Aptr in
B.withUnsafeBufferPointer { Bptr in
C.withUnsafeMutableBufferPointer { Cptr in
for _ in 1…theReps {
vDSP_mmul(Aptr.baseAddress!, IA, Bptr.baseAddress!, IB, Cptr.baseAddress!, IC, M, N, P)
theCount += 1
} } } }
return theCount
Apple describes vDSP_mmul() as performinng “an out-of-place multiplication of two matrices; single precision.” “This function multiplies an M-by-P matrix A by a P-by-N matrix B and stores the results in an M-by-N matrix C.”
Sparse matrix multiplication
var theCount: Float = 0.0
let rowCount = Int32(4)
let columnCount = Int32(4)
let blockCount = 4
let blockSize = UInt8(1)
let rowIndices: [Int32] = [0, 3, 0, 3]
let columnIndices: [Int32] = [0, 0, 3, 3]
let data: [Float] = [1.0, 4.0, 13.0, 16.0]
let A = SparseConvertFromCoordinate(rowCount, columnCount, blockCount, blockSize, SparseAttributes_t(), rowIndices, columnIndices, data)
defer { SparseCleanup(A) }
var xValues: [Float] = [10.0, -1.0, -1.0, 10.0, 100.0, -1.0, -1.0, 100.0]
let yValues = [Float](unsafeUninitializedCapacity: xValues.count) {
resultBuffer, count in
xValues.withUnsafeMutableBufferPointer { denseMatrixPtr in
let X = DenseMatrix_Float(rowCount: 4, columnCount: 2, columnStride: 4, attributes: SparseAttributes_t(), data: denseMatrixPtr.baseAddress!)
let Y = DenseMatrix_Float(rowCount: 4, columnCount: 2, columnStride: 4, attributes: SparseAttributes_t(), data: resultBuffer.baseAddress!)
for _ in 1…theReps {
SparseMultiply(A, X, Y)
theCount += 1
} }
count = xValues.count
}
return theCount
Apple describes SparseMultiply() as performing “the multiply operation Y = AX on a sparse matrix of single-precision, floating-point values.” “Use this function to multiply a sparse matrix by a dense matrix.”
Sparse matrix multiplication
var theCount: Float = 0.0
let inputAValues: [Float] = [ 1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0,
1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0,
1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0 ]
let inputBValues: [Float] = [
1, 2,
3, 4,
1, 2,
3, 4,
1, 2,
3, 4]
var inputADescriptor = BNNSNDArrayDescriptor.allocate(
initializingFrom: inputAValues,
shape: .imageCHW(3, 4, 2))
var inputBDescriptor = BNNSNDArrayDescriptor.allocate(
initializingFrom: inputBValues,
shape: .tensor3DFirstMajor(3, 2, 2))
var outputDescriptor = BNNSNDArrayDescriptor.allocateUninitialized(
scalarType: Float.self,
shape: .imageCHW(inputADescriptor.shape.size.0,
inputADescriptor.shape.size.1,
inputBDescriptor.shape.size.1))
for _ in 1…theReps {
BNNSMatMul(false, false, 1,
&inputADescriptor, &inputBDescriptor, &outputDescriptor, nil, nil)
theCount += 1
}
inputADescriptor.deallocate()
inputBDescriptor.deallocate()
outputDescriptor.deallocate()
return theCount



