Comparing Accelerate performance on Apple silicon and Intel cores
Over the last 18 months, I have been looking at how Apple silicon Macs use their two CPU core types, employing tests that run tight loops of code without accessing memory. So far I have avoided making any comparisons between M-series chips and late Intel processors, as they tell us little about how Apple silicon works. This article brings a change in setting out to compare performance between Intel and Apple silicon Macs, when using Apple’s Accelerate and related libraries for optimum performance across a wide range of hardware. If you’re wondering whether that new M3 Mac you’ve got for Christmas was worth all that money, you might find this useful.
Tests
Several of my tests are crafted in ARM assembly language, but others call on Accelerate and other libraries in macOS, including the four used here:
simd_dot, a vector dot-product function drawn from Apple’s simd library that I believe uses the NEON vector processor when running on M-series chips;
a classical CPU core implementation in Swift of matrix multiplication using 16 x 16 32-bit floating point matrices;
vDSP_mmul, a function from the vDSP sub-library in Accelerate, multiplies two 16 x 16 32-bit floating point matrices, which appears to use the AMX co-processor;
SparseMultiply, a function from Accelerate’s Sparse Solvers, multiplies a sparse and a dense matrix, that I believe uses the AMX co-processor in M-series chips.
Between them, they cover the most popular ways of accelerating non-scalar computation in Apple silicon chips, apart from Compute using the GPU. Source code for each of those tests is given in the Appendix at the end.
Identical Swift source code was used to run these four tests on four contrasting Macs: a well-worn iMac Pro with an Intel Xeon W 8-core processor running at 3.2 GHz, a MacBook Pro (MacBookPro16,1) with an Intel i9 8-core processor running at 2.3 GHz, an Apple Studio M1 Max with 8 P and 2 E cores, and a shiny new MacBook Pro M3 Pro with 6 P and 6 E cores.
Each test consisted of running one or more threads, each of which performs a fixed number of loops of the test calculation:
simd_dot was run in 1-8 threads of 1 x 10^9 loops;
the CPU core matrix multiply was run in 1-4 threads of 1 x 10^8 loops;
vDSP_mmul was run in 1-4 threads of 1 x 10^7 loops;
SparseMultiply was run in 1-4 threads of 1 x 10^8 loops.
Those ensured test times were sufficient for accuracy and reproducibility without taking too long. All tests were run at high QoS, so they were run exclusively on Apple silicon P cores, except for the 7 and 8 thread simd_dot tests on the M3 Pro, which overflowed onto its E cores without significant impact on its linear regression.
Performance times were then used to perform linear regressions of loop throughput (in loops/second) against the number of threads. The gradient of each regression line then gives the overall rate of throughput per thread.
This chart shows two such regressions, for vDSP_mmul and SparseMultiply on the Xeon processor. The gradient of each line is the overall additional throughput obtained by adding another thread of loops, for example when going from 2 to 3 threads. This gives a better picture of core performance than timing single threads, or averaging times for each thread.
Results
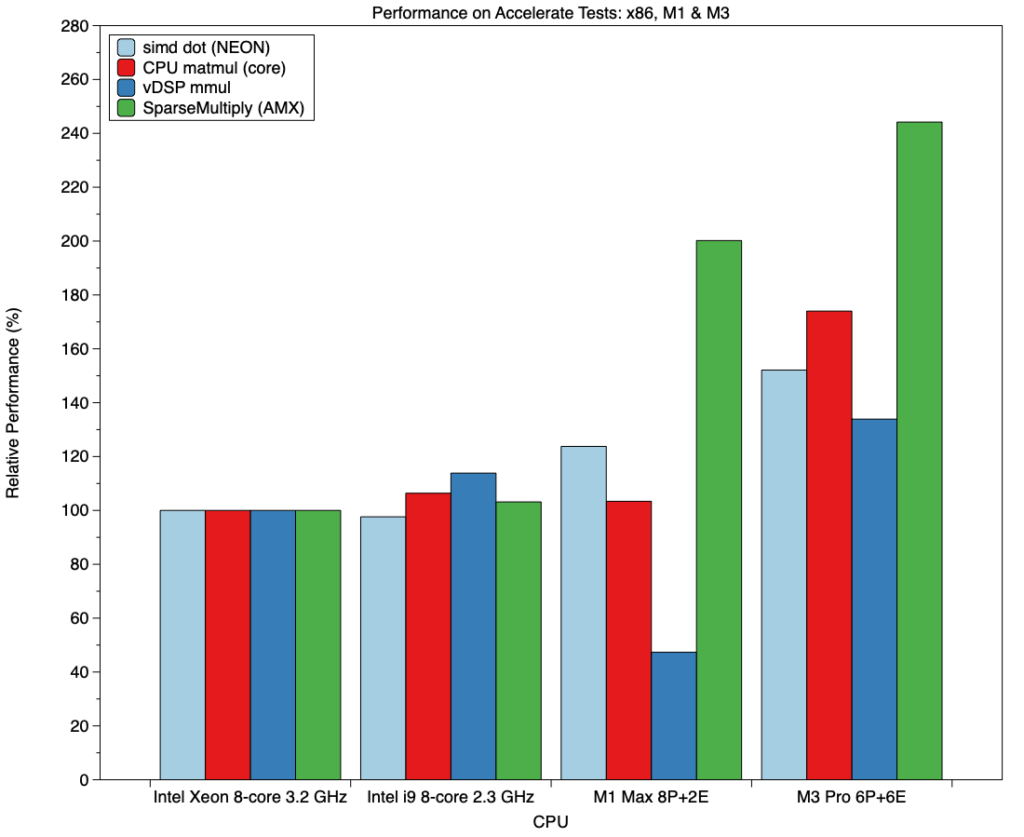
Gradients obtained from linear regression for each test and CPU are given in the table above. There is only one anomalously low value, that for vDSP_mmul on the M1 Max, discussed below. Otherwise, as we’d all hope, results for the M1 Max were similar to or better than the better of the Intel CPUs, and the M3 Pro was the best of all. Those differences are more easily seen in the bar chart below.
For these, the test performances of the Intel Xeon were set at 100%, and results on the other CPUs are expressed relative to those. Differences in the Intel i9 are small: modest improvements in matrix multiplication, greatest when performed using vDSP_mmul. Ignoring for the moment the vDSP_mmul result, the M1 Max was similar in its CPU matrix multiplication, but significantly faster when using the NEON vector processor for simd_dot, and twice the speed for SparseMultiply, probably run on the AMX co-processor. It’s hard to see how that performance could be achieved in the NEON unit or CPU cores alone.
All four tests ran much faster on the M3 Pro, notably simd_dot (152%), CPU matrix multiply (174%) and SparseMultiply (244%). The latter again demonstrates that the performance delivered by Apple silicon cannot be accounted for within its CPU cores, and could only be achieved by external processing, almost certainly in the AMX.
M1 Max and vDSP_mmul
I have previously reported anomalous behaviour of the vDSP_mmul function on the M1 Max chip, and the results here demonstrate how that affects its performance. That appears to result from under-provisioning of CPU cores, a phenomenon only seen in that specific test combination.
Normally, when allocating these test threads at high QoS, macOS first assigns them to P cores in the first cluster of the M1 Pro/Max, until they are all running at high frequency and 100% active residency; it then starts allocating them to cores in the second P cluster, until they’re all at 100%, and finally to the E cores. In the case of vDSP_mmul on the M1 Max, a different scheme emerged, shown in the diagram below.
Not only are the threads allocated to cores to balance numbers between the two clusters, but the number of cores allocated is less than the number of threads, once there are 3 threads or more. That has an inevitable effect on performance, and is largely responsible for poor results for the M1 Max when running vDSP_mmul tests with 3 or more threads. I previously suggested this might be to limit load on AMX co-processors, but I now wonder whether this might be a bug. I will investigate further before raising a Feedback.
Conclusions
Vector and matrix performance on M1 P cores and co-processors are as good if not better than on recent Intel Macs.
Vector and matrix performance on M3 P cores and co-processors far exceeds that of recent Intel Macs.
One matrix multiplication function (vDSP_mmul) may currently show impaired performance on some Apple silicon chips. It’s not yet known whether that’s a bug or by design.
Whichever Mac you’ve got this holiday season, enjoy it, and may your vectors and matrices all work out!
Appendix: Source code
32-bit floating point vector dot-product using simd_dot
var tempA: Float = theA
var vA = simd_float4(theA, theA, theA, theA)
let vB = simd_float4(theB, theB, theB, theB)
let vC = vA + vA
for _ in 1…theReps {
tempA += simd_dot(vA, vB)
vA = vA + vC
}
return tempA
Classical Swift matrix multiplication of 16 x 16 32-bit floating point matrices
var theCount: Float = 0.0
let theMReps = theReps/1000
let rows = 16
let A: [[Float]] = Array(repeating: Array(repeating: 1.234, count: 16), count: 16)
let B: [[Float]] = Array(repeating: Array(repeating: 1.234, count: 16), count: 16)
var C: [[Float]] = Array(repeating: Array(repeating: 0.0, count: 16), count: 16)
for _ in 1…theMReps {
for i in 0..<rows {
for j in 0..<rows {
for k in 0..<rows {
C[i][j] += A[i][k] * B[k][j]
}}}
theCount += 1 }
return theCount
In the ‘classical’ CPU implementation, matrices A, B and C are each 16 x 16 Floats for simplicity, and the following is the loop that is repeated theMReps times for the test. Because of the slow performance of this code, theMReps scales down the number of repeats from millions to thousands.
16 x 16 32-bit floating point matrix multiplication using vDSP_mmul()
var theCount: Float = 0.0
let A = [Float](repeating: 1.234, count: 256)
let IA: vDSP_Stride = 1
let B = [Float](repeating: 1.234, count: 256)
let IB: vDSP_Stride = 1
var C = [Float](repeating: 0.0, count: 256)
let IC: vDSP_Stride = 1
let M: vDSP_Length = 16
let N: vDSP_Length = 16
let P: vDSP_Length = 16
A.withUnsafeBufferPointer { Aptr in
B.withUnsafeBufferPointer { Bptr in
C.withUnsafeMutableBufferPointer { Cptr in
for _ in 1…theReps {
vDSP_mmul(Aptr.baseAddress!, IA, Bptr.baseAddress!, IB, Cptr.baseAddress!, IC, M, N, P)
theCount += 1
} } } }
return theCount
Apple describes vDSP_mmul() as performinng “an out-of-place multiplication of two matrices; single precision.” “This function multiplies an M-by-P matrix A by a P-by-N matrix B and stores the results in an M-by-N matrix C.”
Sparse matrix multiplication using SparseMultiply()
var theCount: Float = 0.0
let rowCount = Int32(4)
let columnCount = Int32(4)
let blockCount = 4
let blockSize = UInt8(1)
let rowIndices: [Int32] = [0, 3, 0, 3]
let columnIndices: [Int32] = [0, 0, 3, 3]
let data: [Float] = [1.0, 4.0, 13.0, 16.0]
let A = SparseConvertFromCoordinate(rowCount, columnCount, blockCount, blockSize, SparseAttributes_t(), rowIndices, columnIndices, data)
defer { SparseCleanup(A) }
var xValues: [Float] = [10.0, -1.0, -1.0, 10.0, 100.0, -1.0, -1.0, 100.0]
let yValues = [Float](unsafeUninitializedCapacity: xValues.count) {
resultBuffer, count in
xValues.withUnsafeMutableBufferPointer { denseMatrixPtr in
let X = DenseMatrix_Float(rowCount: 4, columnCount: 2, columnStride: 4, attributes: SparseAttributes_t(), data: denseMatrixPtr.baseAddress!)
let Y = DenseMatrix_Float(rowCount: 4, columnCount: 2, columnStride: 4, attributes: SparseAttributes_t(), data: resultBuffer.baseAddress!)
for _ in 1…theReps {
SparseMultiply(A, X, Y)
theCount += 1
} }
count = xValues.count
}
return theCount
Apple describes SparseMultiply() as performing “the multiply operation Y = AX on a sparse matrix of single-precision, floating-point values.” “Use this function to multiply a sparse matrix by a dense matrix.”