Explore floating-point number formats in Mints 1.17

Today’s new version of Mints fixes one bug and adds a new feature, the Floating Point Explorer. The bug resulted in incorrect reporting of an old vulnerability in sudo that has long since been fixed in macOS, but was incorrectly reported as being present in some recent versions of macOS.

Mints version 1.17 is now available from here: mints117
from Downloads above, from its Product Page, and via its auto-update mechanism.

For my Saturday morning demonstration, join me in using this new feature, with a twist at the end.

Floating Point Explorer

Most people can get their head around working with integers on computers. PCalc will happily do hexadecimal conversion and arithmetic. Where most of us come unstuck is with floating-point numbers, from which PCalc and pretty well everything else keeps well clear. Although they are more complicated, seeing how they work helps them become more understandable, and that’s what Mints’ new Floating Point Explorer is for.

Computer floating-point formats pack three types of information into their 64 or 32 bits: the sign of the number, and its two values taken from a type of ‘scientific’ notation, like 1.2345 x 10^3 (where ^ means to the power of), sometimes written as 1.2345E3, meaning 1,234.5. Working in decimal is fine for humans, but computers prefer binary, so instead of using powers of 10, they normally use powers of 2. The number itself is referred to as the significand, and the power as the index.

Give this a whirl with Mints’ new Floating Point Explorer window. Think of a number, any number, and enter it into the two boxes along the top row of the window using ‘scientific’ notation.

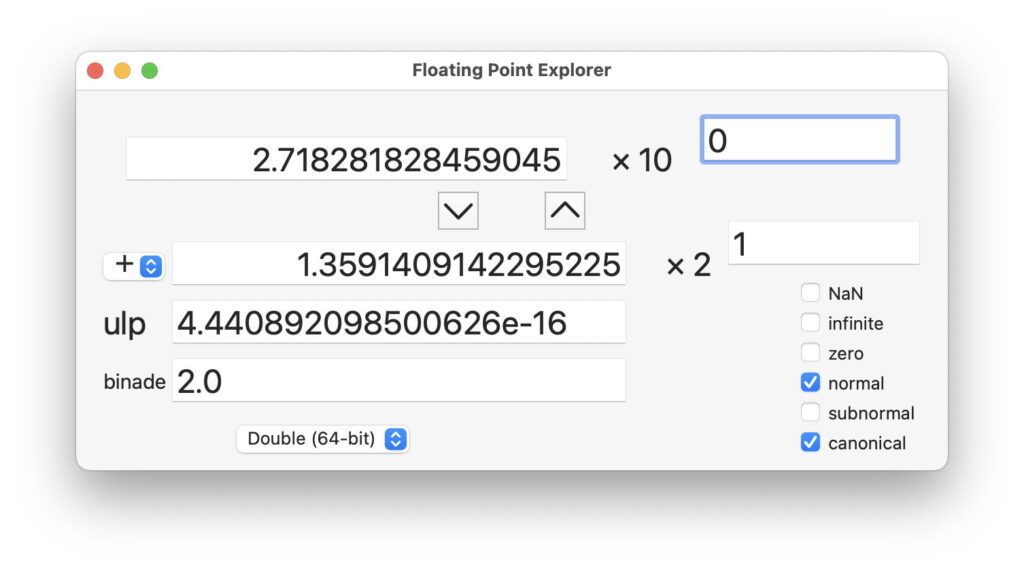
Here I’m entering an approximation of the number e, and put its significand 2.7182… in the left box, and the index, the power of ten, in the box at the upper right, to make the number
2.7182… x 10^0 = 2.7182…

The 10 here is known as the radix of the number. We almost invariably use a radix of 10, as we calculate in decimal, but computers normally use a radix of 2. To see the computer representation of that number as a 64-bit double, click on the down arrow button, or press the down cursor key.

In this case, it’s easy to work out, as 2.0 is 2^1 (two) and 4.0 would be 2^2 (two squared). The answer shown here is thus
1.359… x 2^1

This window provides additional information about that number. The checkboxes at the right show that it’s a ‘normal’ number, and ‘canonical’, so behaves normally with standard precision. That’s given in the box for ulp, which is the difference between this number as a double and the next higher number that can be represented. The binade is different again, and is the radix 10 number given by setting the significand to 1.0 and using the same index, and that should be
1.0 x 2^1
which is of course 2.0.

Now see the effect of expressing that number as a 32-bit single-precision floating-point number. Change the popup menu at the foot to Single (32-bit) and press the down cursor key to convert the value of e to that format. Now the radix 2 conversion is much shorter and the ulp larger, reflecting the loss of precision resulting from using e as a 32-bit floating-point number.

Switch the format back to 64-bit to look at an example of a subnormal number. These are very small floating-point values with lower precision, squeezed in between the smallest normal number and zero. Leaving the radix 10 significand at the top unchanged, set its index to -320 and press the down cursor key.

Using the computer’s radix 2 format, this number is tiny, 1.34… x 2^-1062, and can’t be represented in 64-bit format as a ‘normal’ number. Relative to its size, its ulp is large, at 5 x 10^-324. Make that number smaller still by changing the radix 10 index at the top right from -320 to -325, press the down cursor key, and you’ll see this is represented as zero.

Finally, take this number to 64-bit infinity, by changing the index at the top right to 325 and pressing the down cursor key again.

That’s positive infinity, with an ulp and binade that are not representable, so shown as NaNs, for Not a Number.

What Mints doesn’t do yet is show radix 2 floating-point numbers in hexadecimal, as they might appear in code or memory, or on disk. That would require more work, and I’m unsure at the moment whether there’s any interest in adding that to the next update.

More formats?

Those who know about floating-point number formats will be wondering why Mints only supports 32- and 64-bit formats. macOS and languages like Swift can support the 80-bit extended format still occasionally encountered on the x86 architecture, but that’s not available on Apple silicon Macs, and is rarely used anyway.

There’s also 16-bit floating-point, half-precision, or float16 (but not bfloat16, which is different again). Here’s the surprise, though: according to Apple, this is only supported on its Arm-based chips, and won’t be supported on Intel Macs.

That’s the way the wind now blows.